计算图(Computational Graph)的角度理解反向传播算法(Backpropagation)
计算图
计算图是用来描述计算的语言,是一种将计算形式化的方法。在计算图中,计算被表示成有向图,图中的每一个节点表示一个变量(variable),变量可以是标量(scalar)、向量(vector)、矩阵(matrix)、张量(tensor)等。图中的边表示操作(operation),即一个或多个变量的简单函数。如果变量x经过一个操作f计算得到变量y,那么我们画一条从x到y的有向边。下图是计算图的一个简单例子: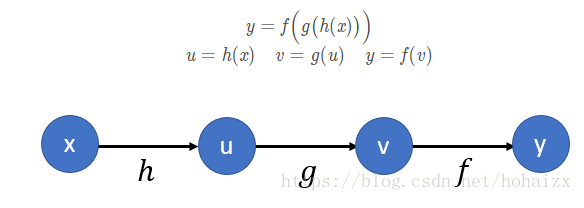
同样我们也可以描述多变量函数,下图展示了Logistic回归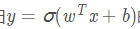 的计算图
的计算图
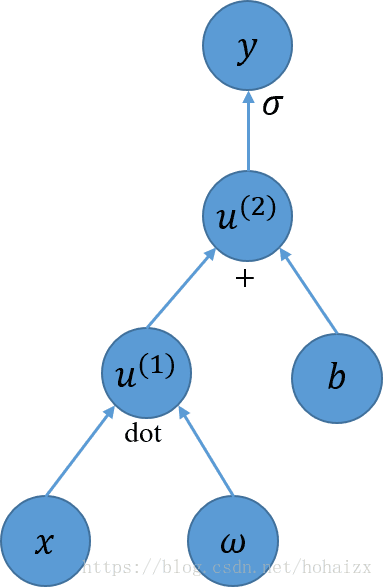
在计算中,有些中间结果在代数表达式中没有名称,但是在图形中是需要的,比如上图中u、v和u^(1)
、u^(2) 。当同一个变量多次出现在代数表达式中时,在计算图中需要将其当作不同的变量对待。例如式子y=xe^(x^2) 的计算图如下
计算表达式的值时,我们从叶子节点开始,顺着有向边逐步归约到根节点即可得到整个表达式的值,可以看作是BP算法的前向传播过程。剩下需要解决的是计算图的求导过程,对应于BP算法的反向传播过程。
首先需要复习下求导的链式法则:
case 1

因为x的变化会带来y的变化,y的变化最终影响z的变化,所以
即图中一个顶点对另一个顶点的导数等于该顶点到另一个顶点的路径上所有导数的乘积。
case 2


下面通过两个例子直观展示下计算图求导过程:
Example 1:e=(a+b)*(b+1)


反向传播算法的计算图

图中x是输入数据,是一个向量,w表示层与层之间的连接权重,是一个矩阵,b表示偏置向量,y是网络的输出,C是损失值,是一个标量。为了计算出参数的梯度,首先需要出每条边的偏导数,因为存在顶点是向量和矩阵的情况,所以涉及到向量对向量的导数和向量对矩阵的导数。
向量对向量的导数
对于标量对向量的导数我们已经会求,推广到向量y对向量x的导数时,我们分步将向量y中每一个元素对向量x求偏导,然后将结果组合成一个矩阵,实际也确实是这样。具体的,假设y是m维向量,xxx是n维向量,将y中每一个元素对x的偏导数横排放成行,最终将形成一个m∗n的矩阵,这个矩阵就是Jacobian矩阵。以Sigmoid函数作为激活函数为例,y和z都是向量,因此∂a/∂z 是一个方阵,

向量对矩阵的导数
m维向量y对m∗n维矩阵x求导也是向量中每一个元素对矩阵中每一个元素求偏导,因此将得到m个m∗n矩阵。这写起来将非常不方便,通常将m∗n矩阵变平为一个向量,因此结果是一个m∗(m×n)的矩阵。以z=wa为例:
依次求出所有边的导数,如下图

最终



